art-patel — radical⇌matter

Our supposedly algorithmic culture is not a material phenomenon so much as a devotional one, a supplication made to the computers people have allowed to replace gods in their minds […].[1]

Metanarrative, metanarrative, high time to kick the habit! (Emergence does not imply transcendence).

acute provocation:

Let ‘Algorithmic Realm’ mean the confluence of networked pervasive sensors, processors and actuators, with ‘artificial intelligence’ (AI)or automated decision making (ADM) systems, as it intersects with our lives.[2] Here, we are concerned more with self-quantification and network surveillance, recommendation algorithms dispensing credit and justice, machine vision for trucks and warriors – less with winning at Go or folding proteins.[3]

This Algorithmic Realm is rooted – radically embedded – in the materialities of mining, refining, and manufacture, of energy transfer and logistics. It is shaped by practices of value extraction, violence to the body and mental slavery; by methods of optimisation, fashions of prediction; it is given form by frameworks of discrimination, languages of regulation, ethical guidelines, the curricula of computer science courses; conventions of individuality and identity are inscribed in it, as are memos issued by the heads of departments of corporate social responsibility.

Algorithms identify and classify (individuals, groups, behaviours, trends), generate and predict; rank, sort, and order (greater than, close to). These processes operate on aggregations and approximations, and are contingent on choices about what constitutes data (figure/ground, signal/noise), what space the data is embedded in, how it is quantified – that is, on underlying mathematical choices. (Mathematics is the art of giving the same name to different things – Henri Poincaré).[4]

Not all algorithms are greedy, but the Algorithmic Realm is.[5] Optimisation is always local – to the writer of the objective function who defines what is ‘good’ and what is ‘good enough’; to the metric that the function employs and the space in which it lives; to a specific moment – sensitive dependence on initial conditions makes it so.

Imperative: Seek strategies to test and protest technological solutionism. How to trouble categories sedimented by habit? Squint!

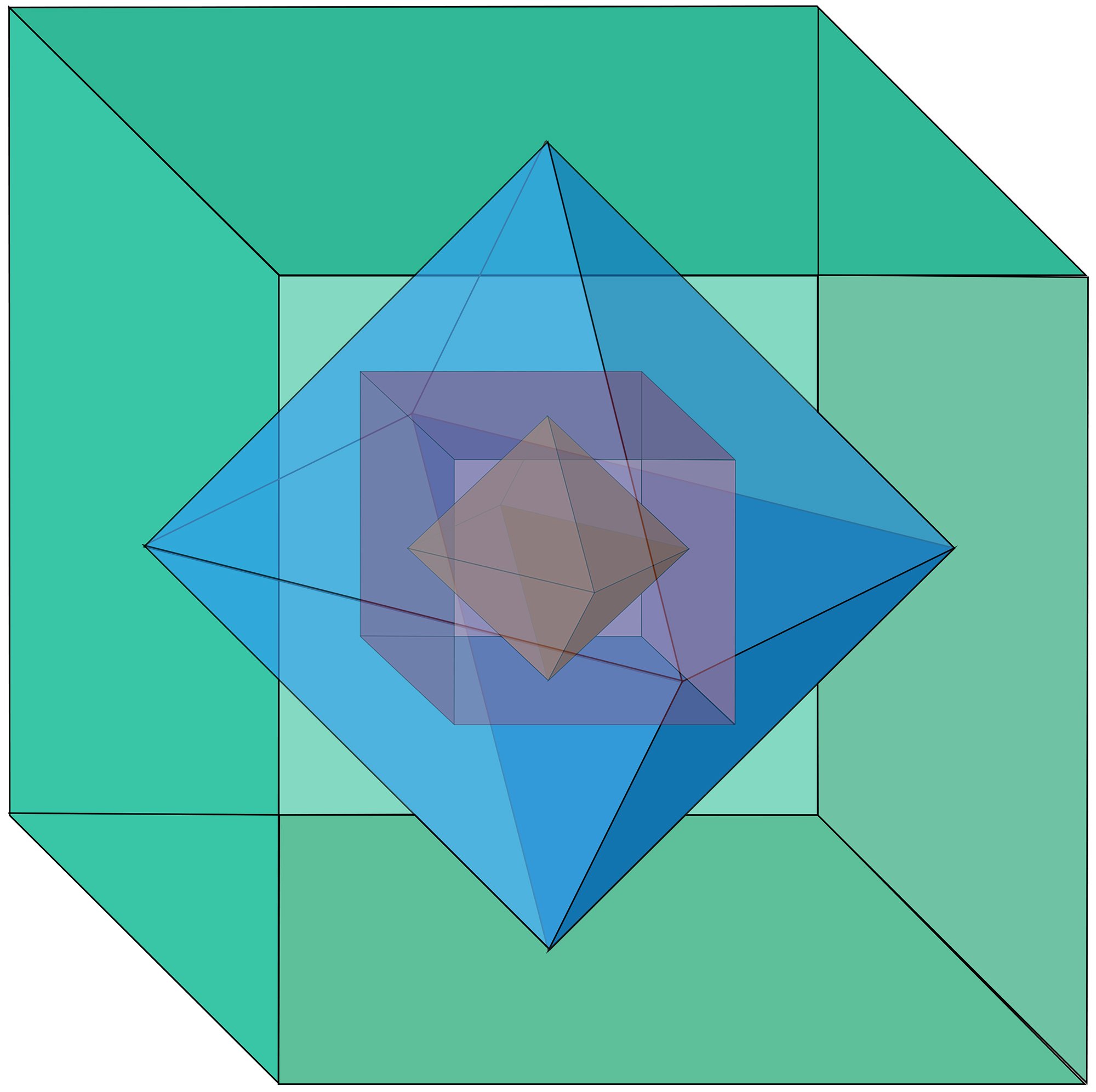
Fig. 1: Dual polyhedra. The cube and the octahedron are duals of each other.

oblique strategy: reflect, rotate, translate, invert, evert [6]

Many structures and concepts in mathematics have corresponding ‘duals’ that are related by well-defined transformations. The green cube and blue octahedron (fig. 1) are duals (each face of the cube corresponds to a vertex of the octahedron), as are the blue octahedron and the pink cube. In projective geometry, theorems become their duals if the words ‘point’ and ‘line’ are swapped.[7] Although such transformations preserve structure, the inversions offer different perspectives.

oblique strategy: fix a different variable

A related move is the swapping of figure and ground, which need not be superficial. Consider a quantity (a figure) measured in some arbitrary unit (the ground). Why fix the ground? In 2018, all the base units of S.I. (Système International) were redefined in terms of physical constants.[8] In theory, universal physical constants such as the speed of light, c, are fixed for all times and places. Historically, numerical values for these constants were obtained through experiment, in units defined with reference to a standard. For example, the metre was originally defined as a convenient fraction of the Earth’s circumference, and later redefined as the length of a physical artefact – a platinum-iridium bar. But as the resolution of instruments and measuring techniques improved, so variations in the standard artefacts became evident. This prompted a philosophical shift – from fixing standardised units and experimentally measuring the constants, to fixing convenient numerical values for the constants and defining units in terms of them. In 1967, the second was defined in terms of the physical constant ∆VCs, the unperturbed ground-state hyperfine transition frequency of the caesium-133 atom, whose numerical value was fixed to be 9 192 631 770 Hz.[9] Subsequently, c was fixed at 299 792 458 ms–1, thus implicitly defining the metre in terms of two physical constants. Through fixing the numerical values of five other constants, the measurement community effected a total figure-ground reversal.

oblique strategy: extend, reframe, tilt-shift

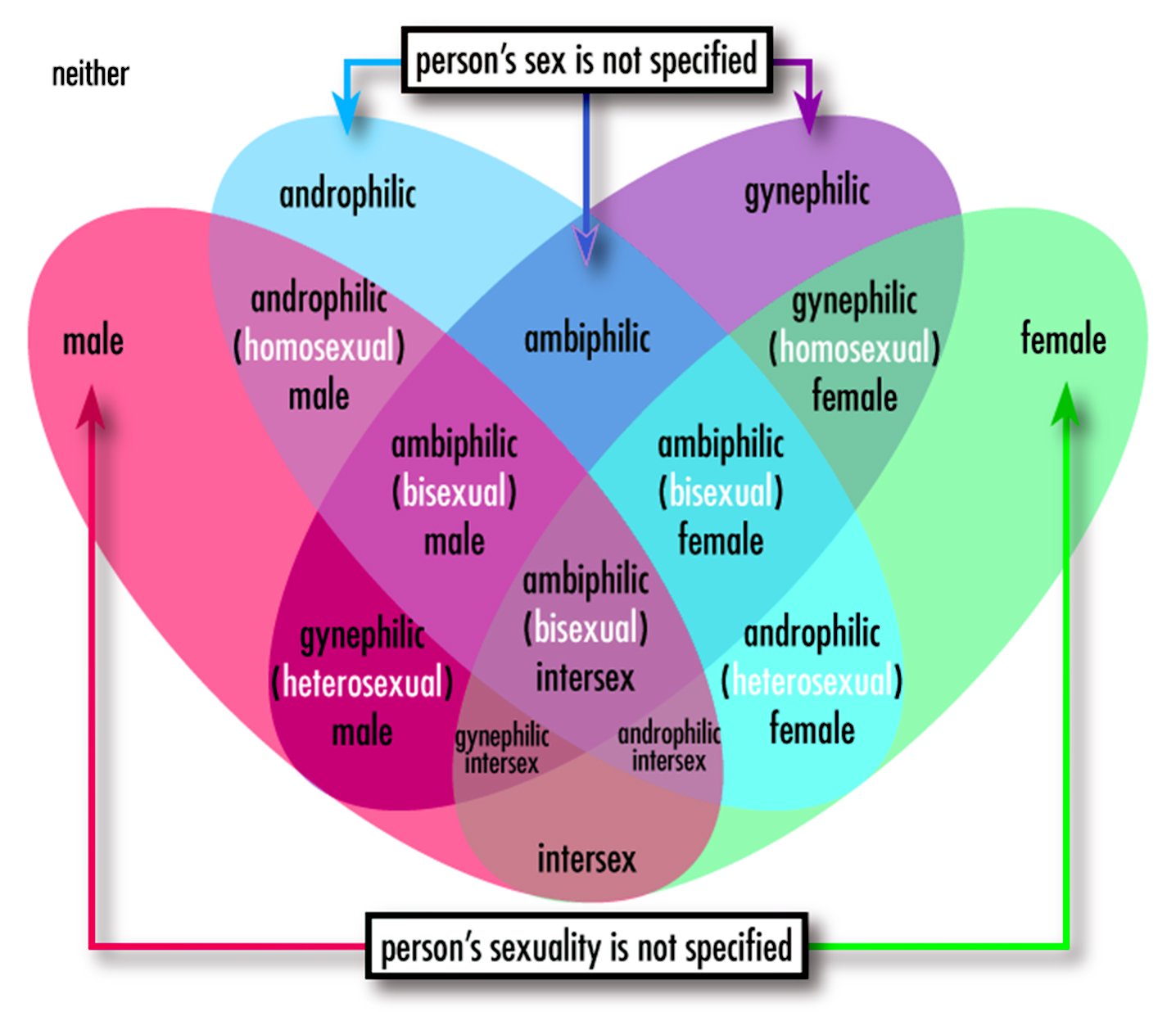
Queer categories, whenever possible. We may want to hold on fondly to categories that were significant in a personal or socio-political struggle, but once they are co-opted or complicated – reformulate! The androphilic-gynephilic schema (fig. 2) expands the homosexual–heterosexual one by decoupling gender identity from sexuality – a candidate for more subtle categorisation.[10]

Fig. 2: Androphilia-gynephilia schema. Illustration modified from Alternative graph of sexuality descriptors and gender identities by Jokestress (CC BY-SA 3.0)

oblique strategy: look at the bigger problem (it might be more tractable)

“Lichens are places where an organism unravels into an ecosystem and where an ecosystem congeals into an organism. They flicker between ‘wholes’ and ‘collections of parts’.”[11] The development of the holistic, relational perspective has transformed microbial ecology, and other sciences.

oblique strategy: process vs. structure

“We have never been individuals.”[12] In his Queer Theory for Lichens, David Andrew Griffiths elaborates a symbiotic view that tacks away from the idea of heterosexual reproduction and inheritance as the dominant mechanisms for propagating life, and challenges outright the concept of the individual that we commonly understand as unproblematic. Ecosystems, colonies, microbiomes; organisms within organisms. The individual has been put in question from other perspectives too – from the point of view of the gene, through the idea of embodied cognition, by the death of the author. Griffiths tunes the study of symbiotic lichens to resonate with contemporary issues in sexual politics: “If heteronormativity and sexual reproduction no longer define the frame through which nature is viewed, then this will have an effect on the definition of some social and cultural practices as ‘natural’.”[13]

queer analogy: exchange parts of speech

Categorically, reframe. “Lichens are a product, less of their parts than of the exchanges between those parts. […T]hey are verbs as well as nouns.”[14]

oblique strategy: traverse the whole tree[15]

More convoluted shifts are possible. Kay Rosen’s The Forest for the Trees is a folding of the lexical and the semantic, a visual pun, an outrageous eversion of language.[16] The work consists of a text painting that reads

tthhee ffoorrreeesstt

in which letters of the phrase ‘for the trees’ are interleaved with those of ‘the forest’. It even rustles like wind through branches. Braid concepts. Translate into another medium – same use (sic). Say music?[17]

queer analogy: reverse of the tapestry

Rethink milk.“The gut microbiota of breastfed infants is modulated by human milk […]’.[18] Oligosaccharides, a major constituent of breast milk, are indigestible by the infant, but constitute food for its intestinal Bifidobacteria infantis – which produce fatty acids, in turn feeding the gut cells. The microbiologist David Mills ‘sees B. infantis as part of milk, albeit a part that is not made in the breast’.[19] What we once thought of as substance or matter produced by mother for infant, we can reframe as a set of relationships between mother, infant, and the infant’s gut microbiome.

Fig. 3: Moiré superlattice. Moiré pattern created by rotating two regular hexagonal lattices through a relative angle of 2.6°.

oblique strategy: out of alignment

When two-dimensional lattices (plane tilings) are superimposed and rotated relative to each other, moiré patterns form. In fig. 3 , there are two copies (green and magenta) of a regular hexagonal lattice, with a relative twist of 2.6°. Out of the regularity of the lattices and their interaction emerges a related regularity – the moiré superlattice, with hexagonal structure at a larger scale.

Graphene is an allotrope (specific atomic arrangement) of the element carbon that occurs in sheets of single-atom thinness, with the atoms arranged at the nodes of a regular hexagonal lattice. When two layers of graphene are stacked and rotated relative to each other at a specific angle, the moiré superlattice that forms exhibits properties that neither layer does alone. For graphene sheets twisted at 1.1°, the resulting superlattice of electrons permeates the sheet-pair so that it becomes a superconductor.[20] At other angles, the graphene acts as an insulator.[21] This dramatic variation in conductivity is an emergent phenomenon. If a quantum analogy is a leap too small, consider the autostereogram.[22] Lay out your categories in patterns, repeated and superposed. Defocus and observe the flux – what depths emerge?

oblique strategy: measure differently

In modelling and algorithm design, mathematical assumptions and choices are inflected by the culture, world-views and mathematical sophistication of system designers, all of which affect data classification, measurement and even (the possibility of) ordering.[23] There exist many (possibly infinitely many, depending on context) equally valid and rigorous methods for computing distance (between points, between numbers), as well as many alternate spaces in which data can be embedded. Is there an obvious ‘natural’ or canonical metric (distance function) or topology (loosely, how the space is connected) for a model or dataset? (What would it mean for a dataset to have ‘natural’ structure, unanchored by teleology?)

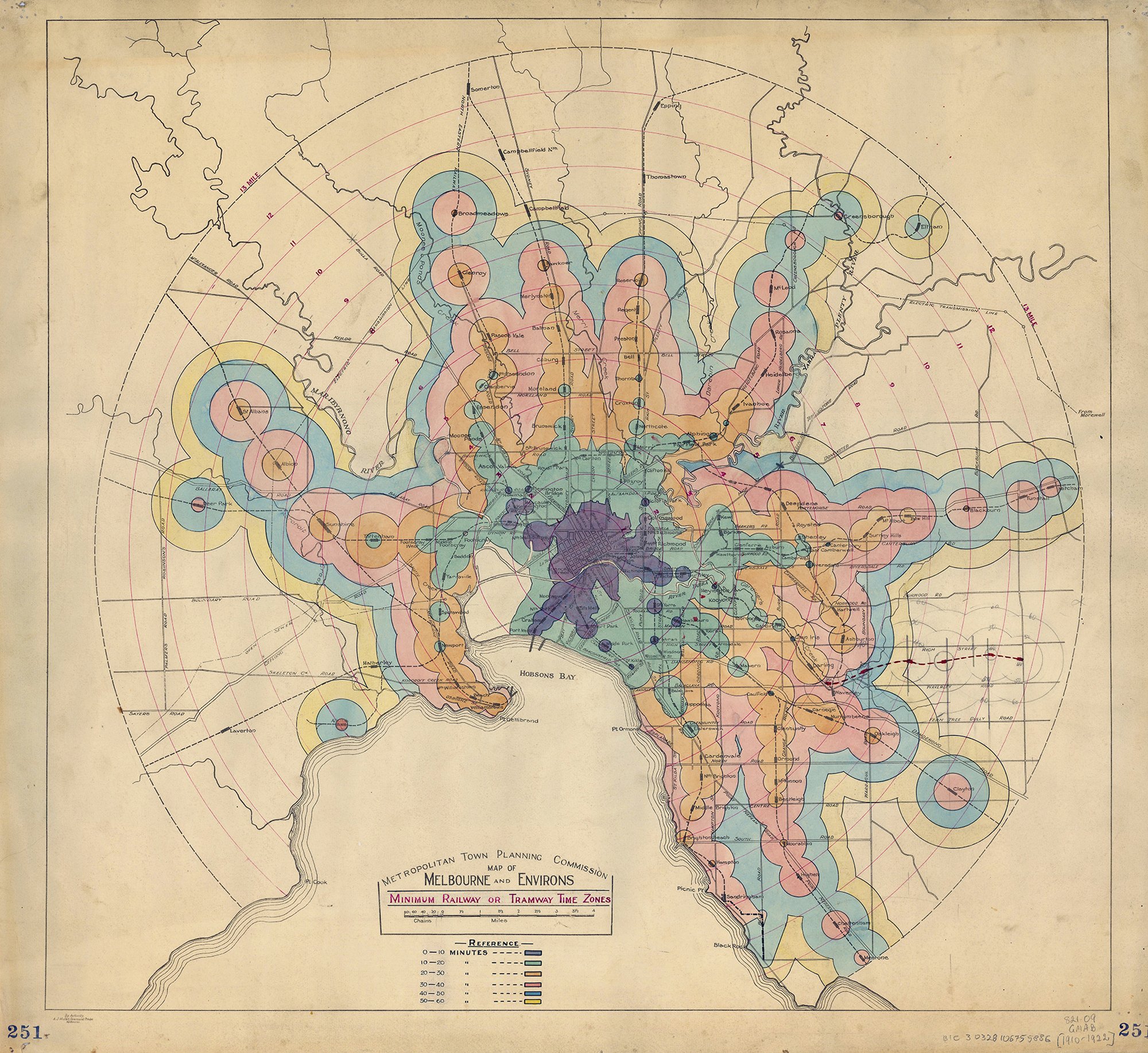
For inhabitants of grid-plan cities (for example: Manhattan), the ‘taxicab metric’ – along streets and up avenues – yields a more useful notion of distance than the normal Euclidean function, that is, the direct path ‘as the crow flies’. An even better metric for commuters is ‘travel time’: the isochrone map for Melbourne’s rail system (fig. 4) uses colour to depict (temporal) distance to the centre. A different isochrone map would hold for travel by road, and for wheelchair and baby buggy users, factors such as pavement surface, street furniture, kerbs and ramps would further skew the map. Urban planning is urban planning relative to a metric.

Fig. 4: Melbourne transit isochrone. Isochrone map of tram and rail transit times from Melbourne city centre, c. 1910–1922. Courtesy of Melbourne and Metropolitan Tramways Board and the State Library of Victoria

Another distance function, the Hamming distance, is the symbol-wise difference between two strings of identical length. The strings ‘1000’ and ‘1001’ have Hamming distance one, because they differ in one symbol; ‘fair’ and ‘foul’ have Hamming distance three; ‘oversight’ (noun form of ‘overseeing’) and ‘oversight’ (noun form of ‘overlooking’) have Hamming distance zero – though semantically they are opposites. Which distance function is appropriate when comparing highly abstract or composite data, such as individual credit scores?

oblique strategy: measure differently (differently)

How big is the number five? The obvious answer is of course correct (‘five’, or ’one more than four’). Formally, the size of a number is captured by its absolute value. By a theorem due to Ostrowski (1916), there exist equally valid definitions of absolute value other than the usual (Archimedean) one; these are the p-adic absolute values, which can be defined for every prime number p.[24] The p-adic absolute value of a number captures information about how divisible it is by p, such that numbers that are highly divisible are relatively small. For example, in 3-adic arithmetic, 3 and 81 are both quite small, while 4 is large (and hence much further away from 3 than 81 is). The provocation advanced here is that the choice of the usual Archimedean absolute value over a p-adic one is arbitrary, and requires contextual justification – just as a choice of metric or topology does.

oblique strategy: try another space (spherical, toroidal, hyperbolic…)

The space that data is embedded in can also dramatically affect interpretation. A naive, one-dimensional plot of political affiliation (left wing – right wing) suggests very different relationships between extreme positions depending on whether it is embedded in a line segment or in an arc (fig. 5). The choice of a particular map projection can mean the difference between life and death (fig. 6).

Fig. 5: One dimension, two embeddings. Embedding the same data in different spaces suggests different relationships.

Fig. 6: Fig. 6: Sea Chase: emergency projection switch. Points that are neighbours under one projection may be distant under another. Sea Chase by Randall Munroe / xkcd (CC BY-NC 2.5) https://xkcd.com/2577/

queer analogy: read the bag, not the contents

Topologically distinct spaces are connected differently, and the same data embedded in different spaces may exhibit different relations of adjacency. Fig. 7 illustrates a demonstration of this. In a classic puzzle of graph theory, three utilities have to be directly connected to each of three houses by non-intersecting paths. This can be solved on a torus (donut with a hole) but not on a sphere or the plane. A variation of this puzzle, in which four worms need to be guided to each of five apples without path-crossing, can be solved on a torus with two (but no fewer) holes. This was printed on a tote bag to accompany the author’s talk, ‘Algorithms in Space’, at the ACM Conference on Fairness, Accountability, and Transparency, Barcelona 2020.

The troubling of categories through the transformations, reframing, alternative metrics and surrogate spaces suggested above operates at the earliest stages of architecture and process design, prior to where much of the current discourse of AI ethics acts (before any consideration of bias due to training data,[25] for example). The Algorithmic Realm is brittle, riddled with contingency, built on silica. Look askance, fiercely.

Fig. 7: Tote bag distributed at the ACM Conference on Fairness, Accountability, and Transparency, Barcelona 2020. Each worm must be connected directly to each apple, without any of the paths intersecting. The task is impossible on a plane, a sphere, or a torus – but it is possible on a torus with two holes, or equivalently, a bag with two handles.

––––––––––––––––––––

Footnotes

[1] Ian Bogost (2015), “The Cathedral of Computation,” The Atlantic, January 15, 2015. At theatlantic.com/technology/archive/2015/01/the-cathedral-of-computation/384300/.

[2] Denis Roio (aka Jaromil) suggests replacing the term ‘artificial intelligence’ with ‘synthetic meaning’; we suggest that ‘synthetic rationalisation’ captures the ontology and causality a little more precisely. Cf: jaromil.dyne.org

[3] Not that AI-powered drug discovery systems are necessarily benign. Flipping a switch (inverting the objective function) of one system led to the generation, in six hours, of 40,000 possible molecules predicted to be more neurotoxic than the nerve agent VX. See: Fabio Urbina, Filippa Lentzos, Cédric Invernizzi and Sean Ekins (2022), “Dual use of artificial-intelligence-powered drug discovery,” in Nature Machine Intelligence, Vol. 4, Mar, 189–91.

[4] Category theory, a foundational approach to mathematics (also increasingly important in computer science and more widely), is perhaps the ultimate formalisation of Poincaré’s insight. Here, ‘category’ refers to a highly abstract collection of ‘objects’ and ‘arrows’, together with some structure and properties. This approach is sometimes called ‘general abstract nonsense’: see Saunders MacLane, ‘The PNAS way back then’, Proc. Natl. Acad. Sci. USA 94 (June 1997): 5983. doi.org/10.1073/pnas.94.12.5983. For a relatively nontechnical introduction, see Eugenia Cheng (2023), The Joy of Abstraction. An Exploration of Math, Category Theory, and Life, (Cambridge).

[5] A greedy algorithm is myopic – it seeks what is immediately optimal. For a characterisation, see for example Paul E. Black (2005), ‘greedy algorithm’, in his Dictionary of Algorithms a

[6] Proposed edits and additions to Peter Schmidt and Brian Eno’s card deck Oblique Strategies, whose various editions are thoroughly documented at rtqe.net/ObliqueStrategies/OSintro.html

[7] Read into this also associated terms, such as ‘collinear’ and ‘concurrent’.

[8] International Bureau of Weights and Measures [BIPM] (2022), Le Système international d’unités, 9e édition, (Paris). bipm.org/documents/20126/41483022/SI-Brochure-9.pdf/fcf090b2-04e6-88cc-1149-c3e029ad8232

[9] ∆νCs never changes. It does not really matter what numerical value we assign to it, because the size of the unit we measure it in is arbitrary. However, we do have an existing, convenient unit – the second – that we wish to refine, so we assign a value that makes the newly defined second as close as possible to the second by the old definition. Instead of having a fixed definition of the second, and measuring ∆νCs relative to it, we fix a convenient number for ∆νCs and define the second relative to that.

[10] Though the classification of gender as male, female, intersex or neither is too rigid; a fluid continuum would be better. For discussion, see for example Henry Rogers (2007), QueerText-u-Realities,Article Press (London/Birmingham).

[11] Merlin Sheldrake (2020), Entangled Life. How Fungi Make our Worlds, Change our Minds, and Shape our Futures, Bodley Head (London), 99.

[12] David Andrew Griffiths (2015), “Queer Theory for Lichens”, UnderCurrents 19: 44. See also Sheldrake’s Entangled Life where he writes: “Lichens are places where an organism unravels into an ecosystem and where an ecosystem congeals into an organism. They flicker between ‘wholes’ and ‘collections of parts’,” in his Entangled Life, 99.

[13] Griffiths, “Queer Theory for Lichens”, 44.

[14] Sheldrake, Entangled Life, 99.

[15] In graph theory, the branch of mathematics that studies graphs (sets of vertices connected by edges), a tree is a graph in which any pair of vertices is connected by exactly one edge. In computing, such tree structures are a widely used abstraction (notably, for machine learning).

[16] Kay Rosen (1990), The Forest for the Trees. Image at kayrosen.com/art/19-forestforthetrees.html

[17] This homophone is to be read aloud. In homage to Rosen's widespread use of homophones, we offer a pair of phrases; the ‘sic’ folded into the first phrase points to the homophonic expression that follows.

[18] Maciej Chichlowski, J. Bruce German, Carlito B. Lebrilla and David A. Mills (2011), “The influence of milk oligosaccharides on microbiota of infants: opportunities for formulas,” in Annual Review Food Science Technology, 332. doi: 10.1146/annurev-food-022510-133743

[19] Ed Yong (2016), I Contain Multitudes. The Microbes With Us and a Grander View of Life, (Penguin), 95.

[20] Y. Cao, V. Fatemi, S. Fang et al (2018), ”Unconventional superconductivity in magic-angle graphene superlattices,” in Nature, 556, 43–50. doi.org/10.1038/nature26160

[21] Y. Cao, V. Fatemi, A. Demir et al (2018), ”Correlated insulator behaviour at half-filling in magic-angle graphene superlattices,” in Nature, 556, 80–84. doi.org/10.1038/nature26154

[22] For the principles behind the autostereogram, see C. W. Tyler and M. B. Clarke (1990), "The Autostereogram", Stereoscopic Displays and Applications, Proc. SPIE Vol. 1258:182–196.

[23] The computational errors that may arise from limitations on precision, or through artefacts of the number base used, or from application of inappropriate versions of a formula are a distinct problem that are beyond the present scope. Such errors can, and have, caused deaths, and deserve scrutiny. For example, on 25 February 1991 in Saudi Arabia, rounding errors in a US Patriot missile defence system led to 25 avoidable fatalities. The Patriot system clock ticks every 0.1 seconds, but 0.1 in binary is a recurring fraction (0.0001100110011…), which was repeatedly rounded until an error built up that was large enough to cause the Patriot to miss an incoming Scud. See the report GAO/IMTEC-92-26: US General Accounting Office (1992), “Patriot Missile Defence: Software Problem Led to System Failure at Dhahran, Saudi Arabia,” (Washington: GAO, Feb 4) at apps.dtic.mil/sti/pdfs/ADA344865.pdf. See also Eyel Weizmann (2012), The Least of All Possible Evils: Humanitarian Violence from Arendt to Gaza, (Verso),ch. 1, where the ‘error’ is not about imprecision or computational error/output of a formula, but the very formula itself.

[24] Ostrowski’s theorem states that every non-trivial absolute value on the field of rational numbers is equivalent to a power of the usual absolute value, or a power of the p-adic absolute value (for some prime p). For the argument above, we make the assumption that computers represent rational numbers, since apart from special applications of exact real arithmetic, a computer can only represent numbers to finite precision.

[25] Not that these critiques are not vital. For examples of just how poorly chosen or designed training data sets can be, see Caroline Criado Perez (2019), Invisible Women. Exposing Data Bias in a World Design for Men, London, (Chatto & Windus) and Cathy O’Neil (2016), Weapons of Math Destruction, New York (Crown Publishing Group).

acute provocations – oblique strategies – queer analogies: how to trouble categories (manifesto)